第1回:消費電力の計算方法について
第2回:出力電流の絶対最大定格について
第3回:ブラシ付DCモータの簡単な駆動について
第4回:PWM駆動による定電流動作について
第5回:PWM駆動の電流回生方法による差について
第6回:モータに最大の電流が流れる状態について
第7回:出力トランジスタの寄生ダイオードを通じて電流回生した時の消費電力について
第8回:モータにトルク負荷をかけた時のモータ電流について
質問:ブラシ付DCモータをPWM駆動する場合に、「PWM周期をモータの電気的時定数より十分短い周期にすること」とありますが、この十分とは「モータの電気的時定数に対して何分の1」等の目安がありますか。
回答:電流リップル値を計算すると、デューティ比 m=0.5 の時が一番大きく、「モータの電気的時定数τ/PWM周期tpwm」と「電流リップル/平均電流」の関係は下表のようになります。
| τ/tpwm | 平均電流 | 電流リップル(p-p) | 電流リップル/平均電流(%) |
|---|---|---|---|
| 100 | 0.5×Ea/R | 0.0025×Ea/R | 0.5 |
| 50 | 0.5×Ea/R | 0.005×Ea/R | 1.0 |
| 25 | 0.5×Ea/R | 0.01×Ea/R | 2.0 |
| 10 | 0.5×Ea/R | 0.025×Ea/R | 5.0 |
| 5 | 0.5×Ea/R | 0.05×Ea/R | 10.0 |
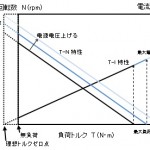
この表から、5%以下のリップル分抑えるためには、τ/tpwmは10倍以上は必要と考えますが、必要な特性に合わせて決める必要があります。数学的には「モータの電気的時定数τに対してPWM周期tpwmが十分小さい」とは tpwm/τ≒0 と考えるため、τ/tpwm>100 程度は必要と考えます。また、わざとリップルを大きくし電流ピークの最大値を上げトルクを大きくするような使用方法もあります。
モータに電源電圧を印加した場合の等価回路図はFig-1のようになります。
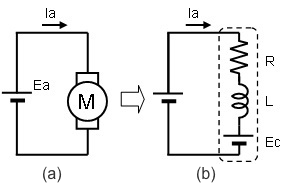 Ea:電源電圧、Ia:モータ電流、R:モータの等価抵抗、
Ea:電源電圧、Ia:モータ電流、R:モータの等価抵抗、
L:モータの等価インダクタンス、Ec:モータの発電電圧
Fig-1 ブラシ付DCモータ電源印加時等価回路
モータ発電電圧 Ec=0V として、モータ等価回路のコイルLと抵抗Rに電圧Eaをステップ状に印加した場合の過渡電流iの関係式は、
L・(di/dt) + R・i = Ea ……(1)
となります。この微分方程式の一般解は、
i = Ea/R + A・exp(-R・t/L) A:初期値 ……(2)
と解けるため、t=0の時にi=i_0の初期値電流が流れているとすると、
A = i_0-Ea/R ……(3)
が求められ、
i = (Ea/R)・(1-exp(-R・t/L)) + i_0・exp(-R・t/L) ……(4)
となります。
モータ端子間をシヨートして電流回生する場合の等価回路はFig-2のようになります。
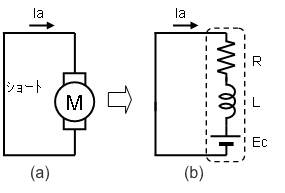 Ia:モータ電流、R:モータの等価抵抗、
Ia:モータ電流、R:モータの等価抵抗、
L:モータの等価インダクタンス、Ec:モータの発電電圧
Fig-2 ブラシ付DCモータ端子間ショート時等価回路
この時の過渡電流iは(2)式でEa=0Vとすればよく、
i = A・exp(-R・t/L) ……(5)
となり、t=0のときにi_0の初期値電流が流れているとすると
A = i_0 ……(6)
が求められ
i = i_0・exp(-R・t/L) ……(7)
です。
これらの式からPWM動作時のモータコイルに流れる過渡電流は、電圧印加時の電流をi_1とすると
i_1 = (Ea/R)・(1-exp(-m・tpwm/τ)) + i_01・exp(-m・tpwm/τ) ……(8)
また、モータ端子間をシヨートして回生する時に流れる電流をi_2とすると
i_2 = i_02・exp(-(1-m)・tpwm/τ) ……(9)
の指数関数となります。
ただし、Ea:印加電圧、R:モータの等価抵抗値、m:オンデューティ比(=0~1)、tpwm:PWM周期、τ:モータ電気的時定数(= L/R)、i_01、i_02:各初期電流値、でモータの発電電圧 Ec=0V としています。
これらの過渡電流式より、モータの時定数に対して十分短い周期のPWMとすると
-m・tpwm/τ ≒ 0 や (-(1-m)・tpwm/τ) ≒ 0
となり、
exp(-m・tpwm/τ) ≒ 1 、 exp(-(1-m)・tpwm/τ) ≒ 1
となるため
i_1 ≒ i_01 、 i_2 ≒ i_02
が成り立ち、常に一定の電流が流れます。
-m・tpwm/τ ≒ 0 や -(1-m)・tpwm/τ ≒ 0
が成り立つには
τ/(m・tpwm) > 100 、 τ/((1-m)・tpwm) > 100
が数学的には必要になり、PWM周期tpwmで考えても
τ/tpwm > 100
程度は必要と考えます。
電流リップルについては電流安定時に、i_2の初期値がi_1となり、i_2の結果がi_1の初期値i_0になるため以下の3式が成り立ちます。
i_1 = (Ea/R)・(1-exp(-m・tpwm/τ)) + i_0・exp(-m・tpwm/τ) ……(10)
i_2 = i_1・exp(-(1-m)・tpwm/τ) ……(11)
i_2 = i_0 ……(12)
i_1とi_2を消去するように式をまとめると、i_0とm、tpwm、τの関係式が求めることができ、パラメータを入れて計算すると各電流値を求めることができます。
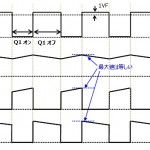
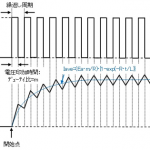
これらの式を使い、モータ電流が0AからPWM駆動した場合の過渡電流波形例をFig-3、Fig-4に示します。Ea=12V、R=6ΩとしてFig-3は τ/tpwm=10、tpwm=100usでmを変化させた時で、m=0.5の時がリップルが大きいです。Fig-4はm=0.5でtpwmを変えることでてτ/tpwmを変化させた時で、τ/tpwmが大きいほうがリップルが小さいです。
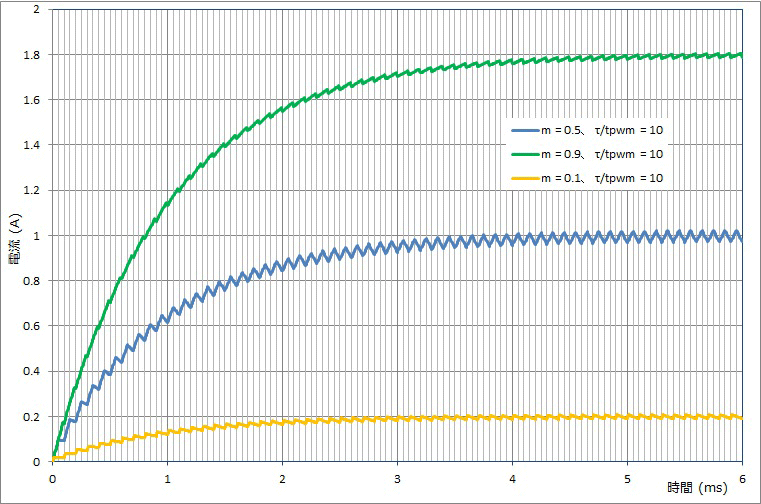
Fig-3 ブラシ付DCモータ PWM駆動過渡電流波形例 m変化時
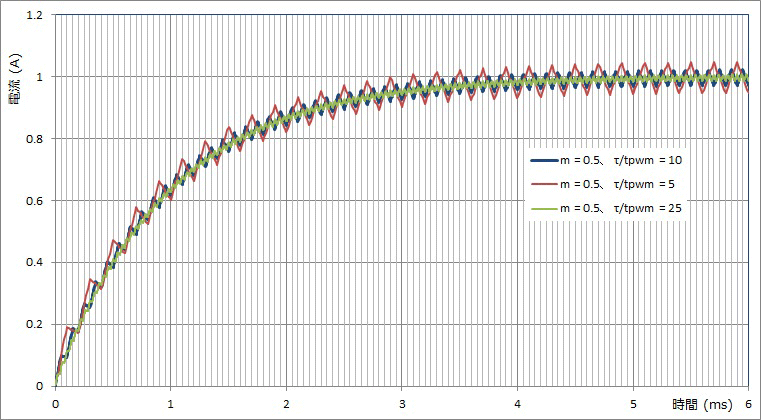
Fig-4 ブラシ付DCモータ PWM駆動過渡電流波形 τ/tpwm変化時
実際には、電源接続時やモータ端子間ショート時には、ドライブ回路の出力のオン抵抗が入ったり、モータ端子間ショート時にダイオードを通ることがあり、それらの考慮も必要になります。
今回の連載の流れ
第1回:消費電力の計算方法について
第2回:出力電流の絶対最大定格について
第3回:ブラシ付DCモータの簡単な駆動について
第4回:PWM駆動による定電流動作について
第5回:PWM駆動の電流回生方法による差について
第6回:モータに最大の電流が流れる状態について
第7回:出力トランジスタの寄生ダイオードを通じて電流回生した時の消費電力について
第8回:モータにトルク負荷をかけた時のモータ電流について
第9回:モータの電気的時定数に対して十分に小さいPWM周期について(今回)
第10回:1個のMOSFETでモータをPWM駆動させるときのモータに並列接続するダイオードに流れる電流について