消費電力の計算方法について

「モータドライバ博士のQ&A」では、よくあるお問い合わせを元に、ロボット製作者、エンジニアのみなさんに役に立つ技術解説を発信していきます。回答するのは、ローム株式会社モータドライバ開発課の藤井さん。名古屋工業大学電子工学科卒業後、ローム株式会社へ入社し、これまで数々の開発に取り組んできたモータードライバ一筋のエンジニアです。
第1回は、ブラシ付モータドライバの消費電力計算方法について回答します！

質問：ブラシ付モータドライバの消費電力計算ですが、(LSIの回路電流＋モータに流れる電流)×電源電圧でよいのでしょうか？

回答：(モータに流れる電流×電源電圧)ではモータの消費電力も含んでしまうため、ドライバの消費電力\(Pc\)を求める計算は定電圧で駆動している場合、基本的には

\[
Pc = 小信号部回路電流 \times 電源電圧 + モータに流れる電流 \times (上側出力間電圧 + 下側出力間電圧)
\]

になります。

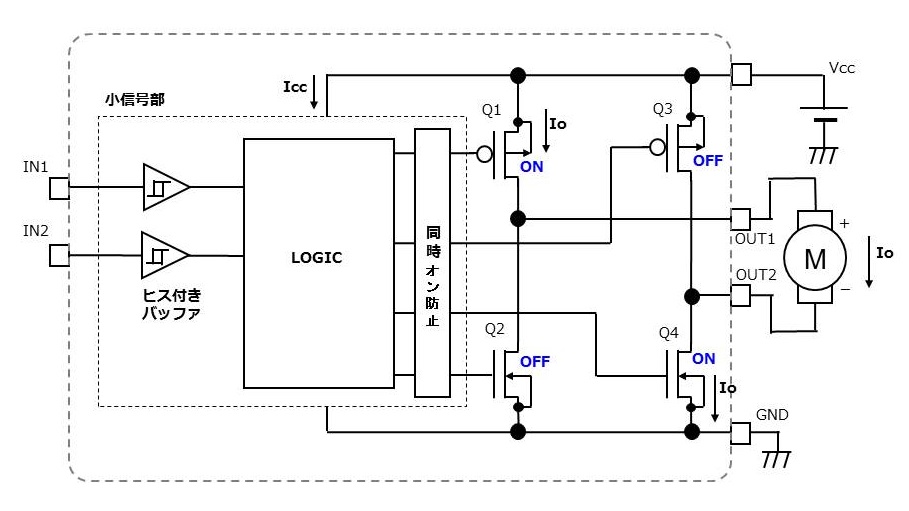
Fig-1 消費電力計算等価回路例

Fig-1の回路例で小信号部回路電流を\(Icc\)、電源電圧を\(Vcc\)、モータに流れる電流を\(Io\)、とします。
MOS出力は抵抗値で特性が表されるため、オンしている上側出力Q1のオン抵抗を\(RonH\)、オンしている下側出力Q4のオン抵抗を\(RonL\)とすると、

上側出力間電圧 \(VH = Io \times RonH\)
下側出力間電圧 \(VL = Io \times RonL\)

となります。

これにより消費電力\(Pc\)は
\[
Pc = Icc \times Vcc + Io \times (VH + VL) = Icc \times Vcc + Io^2 \times (RonH + RonL)
\]

になります。

＜PWM駆動時の消費電力について＞

Fig-2 PWM動作等価回路

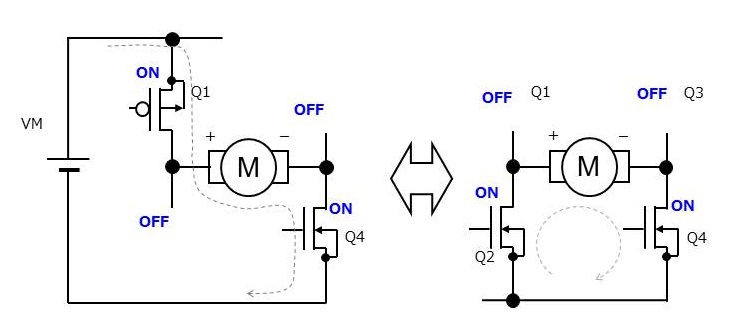
（左）a.電圧印加時　(右）b.電流回生時

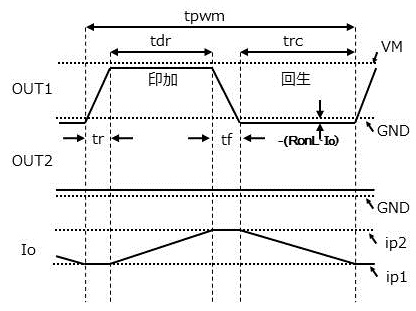
Fig-3 動作電圧電流波形等価

• \(tr\)：ローからハイに遷移する時間
• \(tdr\)：ハイを維持し電流を供給する時間
• \(tf\)：ハイからローに遷移する時間
• \(trc\)：ローを維持し電流を回生する時間

の4つの部分に分かれ、もう片方の出力OUT2は常にローの動作になります。

簡単に考えるためこれらの動作で出力がハイからローまたはローからハイへの電圧変化は直線でその間電流は一定とします。また、印加時と回生時の電流変化も直線とします。(Fig-3参照)

電圧変化部分の消費エネルギーは電圧の時間関数と電流の時間関数の積を各時間で積分し、電流変化部分の消費電力は電流の時間関数の２乗と抵抗の積を各時間で積分すると求めることができます。

\(tr\)部分の消費エネルギー：\(Er\)は
\[
Er ≒ \frac{1}{2} ip1 \times VM \times tr + (ip1)^2 \times RonL \times tr
\]

\(tf\)部分の消費エネルギー：\(Ef\)は
\[
Ef ≒ \frac{1}{2} ip2 \times VM \times tf + (ip2)^2 \times RonL \times tf
\]

\(tdr\)部分の消費エネルギー：\(Edr\)は
\[
Edr ≒ \frac{1}{3} \{(ip1)^2 + ip1 \times ip2 + (ip2)^2\} \times (RonH + RonL) \times tdr
\]

\(trc\)部分の消費エネルギー：\(Erc\)は
\[
Erc ≒ \frac{1}{3} \{(ip1)^2 + ip1 \times ip2 + (ip2)^2\} \times (2 \times RonL) \times trc
\]

となります。

出力の消費電力\(Pc\_ot\)はこの4つの部分を合計し全体の時間で割ると求められ、
\[
Pc\_ot ≒ \frac{(Er + Edr + Ef + Erc)}{tpwm}
\]
になります。

これに出力電流以外に電源が供給する回路電流\(Icc\)と電源電圧\(Vcc\)の積を加えると全体の消費電力\(Pc\)になり
\[
Pc ≒ Pc\_ot + Vcc \times Icc
\]
です。

\(tr\)と\(tf\)が\(tpwm\)に対して十分小さく、電流変化がほとんどなく\(ip1 = ip2\)の場合、電力は
\[
Pc ≒ (ip1)^2 \times \{(RonH + RonL) \frac{tdr}{tpwm} + (2 \times RonL) \frac{trc}{tpwm}\} + Vcc \times Icc
\]
となり、駆動時と回生時とで変わる電流経路による発生電力の\(PWM\)一周期時間に対する駆動時間と回生時間の比率の合計になります。

今回の連載の流れ

第1回：消費電力の計算方法について（今回）
第2回：出力電流の絶対最大定格について
第3回：ブラシ付DCモータの簡単な駆動について
第4回：ＰＷＭ駆動による定電流動作について
第5回：PWM駆動の電流回生方法による差について
第6回：モータに最大の電流が流れる状態について
第7回：出力トランジスタの寄生ダイオードを通じて電流回生した時の消費電力について
第8回：モータにトルク負荷をかけた時のモータ電流について
第9回：モータの電気的時定数に対して十分に小さいPWM周期について
第10回：1個のMOSFETでモータをPWM駆動させるときのモータに並列接続するダイオードに流れる電流について