抵抗の値を変えたら、なんか動いた(その1)
電子工作をしていると「理屈はともかく、こうしておけ」と説明されるものがけっこうあります。とりあえず動くものをつくる分にはあまり困らないことが多いですが、「なんで?」とモヤモヤする方も多いかと思います。あるいはうまく動かないとき、闇雲に適当に手を入れて、とりあえず動いたからまあいいか、としている場合もあるのではないでしょうか。より踏み込んだ電子回路をつくるようになると、それらの「理屈」がけっこう効いてくる場面もあります。
このシリーズでは、そんな場面のいくつかについて、背景の理論を知り、深く理解していこうと思います。
目次
①はじめに
電子工作をしていると、抵抗を使う場面がたくさんあります。一番身近なのは、LEDにつなぐ電流制限抵抗でしょうか。「とりあえず1kΩをつなげばOK」と言われた経験がある方も多いかと思います。理屈はよくわからなくても「そういうもの」と受け入れて、つないでいる方も多そうです。
実際、それで困ることはあまりありません。
とはいえ「なんで抵抗、それも1kΩをつなぐのだろう?」とモヤモヤしている方は多いかと思います。
また、うまく動かないときに、とりあえず適当に抵抗やコンデンサをつけて「一応動いたからOK」としてしまう場面も珍しくはありません。とはいえ理屈がわかっていないと、また動かなくなったときにお手上げになってしまいます。
まさに「なにもしてないのにこわれました」、あるいは「なにもしてないのに動きました」です。
今回は3回にわたって、電子回路の中で抵抗を使う場面とその理論から、抵抗を入れる意味とその値の求め方をみていきます。
②LEDの電流制限抵抗の近似的な求め方
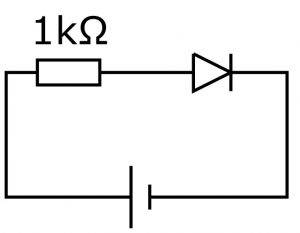
LEDを電源につないで点灯するとき、よく「1kΩの抵抗を直列につなぐ」と説明されます。この抵抗は、LEDに流れる電流をちょうどよい値にする役割があることから「電流制限抵抗」といいます。
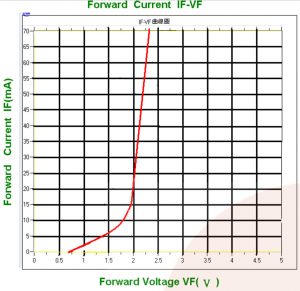
LEDの電圧-電流特性とその近似(1L0531Y22C0CA204のデータシートより)
電流制限抵抗の求め方は「LEDの順方向電圧が一定」という仮定を使うと、割と簡単に求められます。電子回路の理論は、つきつめれば「加える電圧と流れる電流の関係」です。LEDに加える電圧と流れる電流の関係は1枚目の図のようになります。
LEDに流れる電流が多いほど明るく点灯しますが、あまり流しすぎると焼き切れてしまいます。実際に流すべき電流は使うLEDによって異なるので、詳しくはデータシートを読んだり、点灯させて明るさを確認して決めることになりますが、5〜10mAが妥当な場合が多いようです。
グラフを見てみましょう。LEDに加える電圧をあげていくと、1.5Vくらいから急激に電流が流れ始めて2Vくらいでほとんど増えなくなります。これをすごく大ざっぱに近似すると、「電流が流れ始めたら電圧は2Vで一定」とみることができます。つまり「電流が流れているLEDは2Vの電圧源(電源)」というわけです。
では実際に流れる電流はいくらになるのかというと、それにつなぐ周りの回路から決まります。
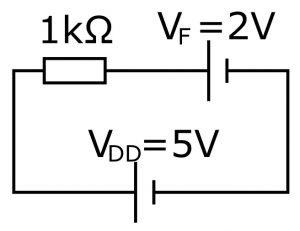
電流が流れているLEDを電圧源とみなして電流を求める
LEDに電流制限抵抗をつないだ回路では、この図のように考えることができます。この場合のLEDに流れる電流は抵抗を流れる電流と同じなので、電流はオームの法則、つまり「抵抗を流れる電流は、両端の電圧の差を抵抗で割ったもの」から求めることができます。
けっこう大ざっぱな近似を使っているのですが、実際の場面でもある程度は正確に求めることができるので、実用上は十分なことが多いです。ここで電源電圧を5V、電流制限抵抗を1kΩとし、LEDを2Vの電圧源とみなせば抵抗の両端電圧は5-2=3Vですから、LEDと抵抗を流れる電流は3V/1kΩ=3mAとなります。
③LEDの電流制限抵抗と負荷線
近似を使わずにLEDを流れる電流を求めるのは、実はけっこう複雑な問題です。というのも、LEDを流れる電流はLEDの両端電圧によって変わり、その両端電圧は電流制限抵抗の両端電圧によって変わります。つまりLEDと電流制限抵抗の2つの素子において、それぞれ電流と電圧が変わりうるので、両者を同時に求めることになるということです。実際には、それらがつりあう「ちょうどいいところ」の電圧・電流となるわけですが、それを求める方法が「負荷線」という考え方です。
LEDを流れる電流は電流制限抵抗を流れる電流と同じなので、これをIとおきます(キルヒホッフの第1法則)。LEDの両端電圧をVLEDとすると、抵抗の両端電圧VRは(VDD – VLED)(キルヒホッフの第2法則)。オームの法則から、VRと電流Iの関係はVR=I・Rとなり、これらを使うと、LEDを流れる電流と両端電圧VLEDの関係は次の式になります。
I = 1/R・(VDD -VLED)・・・(1)
これは、LEDの電圧と電流の関係式なわけですが、LED自身の特性として、電圧と電流の関係はさきほどのグラフの関係でもあることがわかっています。つまりLEDの「電圧と電流が満たすべき関係」を2つの方法で表せたわけですが、実際の電圧と電流は、この2つの関係を満たす値、ということです。
数学的に考えると連立方程式ができあがり、方程式を解けば求められるわけですが、この場合は一方の電圧-電流の関係が式ではなくてグラフで表されています。であれば両方ともグラフで描いて、その交点をもとめればよいわけです。交点は、2つの関係(のグラフ)を同時に満たすところ、だからです。
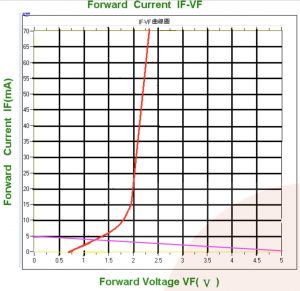
LEDの電圧-電流特性のグラフと負荷線(1L0531Y22C0CA204のデータシートより)
この関係の場合、1つの式(1)は横軸をVLED、縦軸をIとすれば直線のグラフができます。具体的にはVLED=0のときはI=VDD/R、VLED=VDDのときはI=0なので、(I, VDD)=(VDD/R, 0)と(0, VDD)の2つの点を通る直線となります。これをもう1つの電圧-電流の関係である、LEDの電圧-電流特性のグラフに重ねて描くと、例えばR=1kΩ、VDD=5Vの場合、図の紫の線のようになります。この2つのグラフの交点は、グラフから(4mA, 1.2V)と読み取れますので、I=4mAが実際にこの回路でLEDに流れる電流ということです。この式(1)を「負荷線」と呼びます。
④フォトカプラとトランジスタの負荷抵抗
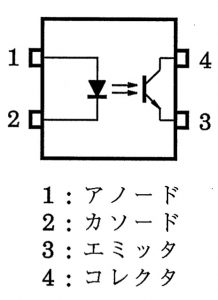
フォトカプラTLP785(TLP785のデータシートより)
絶縁された信号伝送をする場合に使われる電子部品に「フォトカプラ」があります。これは送信側のLEDからの光を受けて、流れる電流を増幅するトランジスタ(フォトトランジスタ)を受信側とする素子で、送信側と受信側が電気的につながっていないものです。
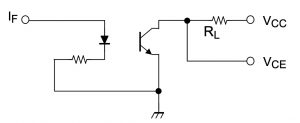
フォトカプラTLP785の使用回路(TLP785のデータシートより)
このフォトカプラの送信側はLEDですから、先ほどの電流制限抵抗で流れる電流を決めることができます。では受信側のトランジスタの出力はどのように取り出せばよいのでしょうか。TLP785のデータシートに、特性評価回路としてこのような回路図が載っています。電子回路の用語だとエミッタ接地回路と呼ばれる回路ですが、このコレクタの電圧VCEを出力電圧とみなすわけです。
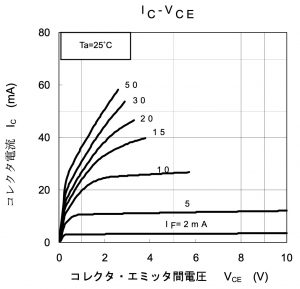
フォトカプラTLP785のIC-VCE特性(TLP785のデータシートより)
このVCEとコレクタを流れる電流ICの関係は、データシートにこのようなグラフが載っています。一方、VCEとICは、さきほどのLEDのときと同じように考えると、オームの法則からVCE + R・IC = VCCという関係が成り立つのです。
これを変形すると次のような式になります。
IC = 1/R・(VCC – VCE)
これはまさしく負荷線で、LEDの場合と同じようにグラフに重ねて描いて、それらの交点を求めれば、ICやVCEが求められそうです。
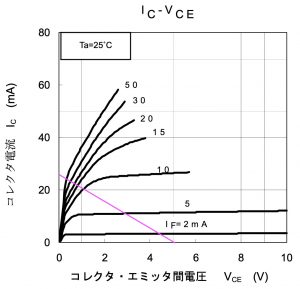
フォトカプラTLP785のIC-VCE特性と負荷線(TLP785のデータシートより)
VCC=5V、RL=2kΩとして求めた負荷線を描くと、図のように(IC, VCC)=(0mA, 5V), (25mA, 0V)を通る直線となります。しかしさきほどのLEDの場合と異なるのは、元のIC-VCEの関係のグラフが複数あるということ。これは受信側のトランジスタのICとVCEの関係が、送信側のLEDに流す電流IF(とそれにあわせて放出される光の強さ)によって変わるためです。
つまり送信側のLEDの電流IFを変えると、それにあわせてトランジスタのICとVCEの関係式が変わるわけです。実際のICとVCEは、グラフと負荷線との交点として求められますから、IFを変えるとVCEが変わっていく様子をグラフ上の交点の移動としてみることができます。
IF=10mAとするとVCEは約1Vとなることがわかります。ちなみにこのグラフでは、送信側のLEDの電流IFが0のときのグラフがありませんが、LEDに電流が流れなければ受信側のフォトトランジスタにも電流は流れずIC=0のはずなので、VCE=5Vです。
送信側でLEDに電圧を加えて電流を流す”1”だと、出力VCE=1V、つまり低い電圧”0”となり、LEDに電流を流さない”0”のときはVCE=5V、つまり高い電圧”1”となります。論理的にはNOTゲートとして働くことになりますね。
実際のLED電流制限抵抗やRLは、全体の消費電流や両者に流せる電流の上限、トランジスタが”ON”のときのVCEの電圧がどこまで下がるべきか、および詳しくは今回説明しませんでした。これらは”0”と”1”の間の変化にかかる時間(スイッチング時間)から決めることになります。
このように負荷線は、慣れるまではちょっと面倒に思えますが、回路の詳しい動作を理解する便利な方法です。実際に回路を動かして、特に動作が怪しいな、と思う場合は、信号電圧をオシロなどで観測しながら、その値を見直すとよいでしょう。
⑤プルアップ・プルダウン抵抗
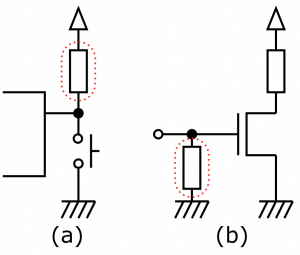
プルアップ抵抗(a)とプルダウン抵抗(b)の例
もう1つ、電子工作をしていると使う場面が多いのが「プルアップ抵抗」または「プルダウン抵抗」。プルアップ抵抗は、文字通りこの図の(a)のように、ある端子を高い電圧(ほとんどの場合は電源電圧)に引っ張り上げる(pull-up)形につなぐ抵抗です。逆にプルダウンはこの図の(b)のように低い電圧(ほとんどの場合はGNDの0V)に引き下げる(pull-down)ようにつなぐ抵抗です。
これらは、その端子が他のどことも抵抗や導線でつながっていない場合に、その電圧を決めるために使います。この(a)の場合、プルアップ抵抗がないと、スイッチがOFFのときには左側のマイコンの入力端子はどこともつながっていない状態となります。このような状態では、端子は浮いた状態で、電圧を「決める」方法がありません。コンデンサの片方がどこともつながっていない場合、その電圧は中に蓄えられる電荷によって決まります。ですが、マイコンの入力端子の等価的なコンデンサが充電されているか放電されているかの状態しか電圧を決める方法がなく、例えば手を近づけると電荷が誘起されて電圧が変わる、といったことが起こってしまう可能性があります。
そこでプルダウン抵抗をつなぐと、この端子に電流が流れる経路ができるので(この状態を「直流的に」と呼びます)、電圧が決まります。この場合は、マイコンの入力端子には電流が流れませんから、スイッチがOFFのときはプルアップ抵抗に電流は流れません。 抵抗の両端電圧はオームの法則から0Vとなります(V=IRでI=0なのでV=0)から、端子は電源電圧と同じ電圧、つまり”1″になります。スイッチをONにするとプルアップ抵抗がGNDにつながった状態になりますが、スイッチがONのときの抵抗はほぼ0Ωとみなせますから、端子の電圧はほぼ0V、つまり”0″となります。
このスイッチのように、動作時の抵抗が0Ωとみなせる場合は、プルアップ抵抗やプルダウン抵抗の値は、どのような値でも構いません。とはいえ動作時にはその値に応じた電流が流れますので、あまり小さい値は消費電流の観点から得策ではありません。一般的には10kΩから100kΩを使うのが一般的のようです。
しかし、動作時の抵抗が0Ωとみなせない場合は、プルアップ抵抗・プルダウン抵抗の値には注意をする必要がありあす。
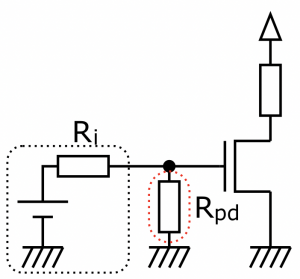
例えばこの図のように、内部抵抗Riが無視できない信号源で、プルダウン抵抗Rpdをもつ回路を駆動する場合で考えましょう。内部抵抗Riが大きいということは、信号源から電流を流すほど、外に出てくる(外で観測される)電圧が下がってしまう、ということです。これは流れる電流に比例した電圧が内部抵抗Riの両端に発生するため、その分、外に出てくる電圧が下がる(電圧降下と呼びます)わけです。
この回路の場合、回路の入力電圧であるプルダウン抵抗Rpdの上側の電圧は、信号源の電圧とRiとRpdによる分圧となります。
例えばRiが10kΩと大きい信号源の場合にRpd=10kΩとすると、回路の入力電圧は信号源の電圧の半分となってしまい、場合によっては十分に”1″とみなせない、つまり十分にONとならず電流がちゃんと流れないような中途半端の状態になってしまいます。このような場合はプルダウン抵抗Rpdをもっと大きな値、つまり信号源の内部抵抗Riよりも十分大きな値、例えば100kΩとすれば大丈夫です。とはいえプルダウン抵抗Rpdを100MΩのようなあまり大きい値にしてしまうと、事実上「直流的に」つながっていないことになりますので、電圧を固定するプルダウンの効果がなくなってしまいます。そこそこの値にはするべきです。
このようにプルダウン抵抗も、周りの回路によって適切な値が決まりますので、実際に使う場面に応じて、特に動作が怪しいな、と思う場合は、入力端子の電圧をオシロなどで観測しながら、その値を見直すとよいでしょう。
今回はここまで。次回もお楽しみに!
今回の連載の流れ
第1回:抵抗の値を変えたら、なんか動いた(その1)(今回)
第2回:抵抗の値を変えたら、なんか動いた(その2)
第3回:抵抗の値を変えたら、なんか動いた(その3)








