抵抗の値を変えたら、なんか動いた(その3)
第1回:抵抗の値を変えたら、なんか動いた(その1)
第2回:抵抗の値を変えたら、なんか動いた(その2)
第2回では、「電圧や電流が、時間とともにどう変化するか」という観点で、電子回路の挙動と抵抗の働きについてみてきました。最終回となる今回は、それと似た見方として、電圧や電流が、周波数によってどう変化するか、そしてそこに抵抗がどう関係してくるか、という観点で電子回路の働きを見ていこうと思います。
目次
①周波数領域での考え方
時間とともに変化する信号に対し、電子回路がどのようなふるまいをするかについて、第2回では回路が変化に追従する速さという観点、いわゆる過渡応答としてみてきました。これとは別の見方として、「変化している状態がずっと続いている状態」という見方があります。
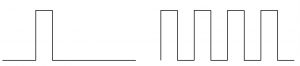
単発の信号(左)と、「時間とともに変化」の定常状態(右)
変化する信号といっても、例えばスイッチを押したときの電圧波形、のような単発の信号もありますが、時間とともに規則的にずっと変化し続ける信号、というのもあります。正弦波のパターンで変化し続ける信号であれば、「時間とともに変化する」という状態が定常的である、ということです。周期的な変化(ワンパターンの変化)が、過去も未来も続くので、電子回路の振る舞いも、それにあわせて周期的になります。
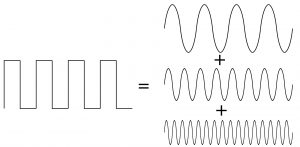
周期的な信号は正弦波に分解することができる
周期的な変化は、数学的には正弦波で考えることができます。もちろん周期的に変化する信号には、方形波のような、正弦波ではない波形もあるのですが、「フーリエ展開」という数学テクニックを使うと、いろいろな周波数・周期の正弦波に分解することが可能です。
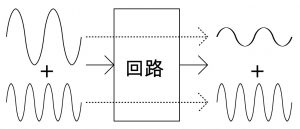
分解した正弦波のそれぞれに対して電子回路がはたらく
そして分解したそれぞれの正弦波に対して、電子回路がはたらいて出てくる出力を考えることができるわけですが、実際の出力も、それぞれの正弦波に対する出力を合成(加算)したものと考えることが、実はできます。当たり前のように感じる方も多いかと思うのですが、実はけっこう奥が深い話で、「重ね合わせの原理」と呼ばれています。というわけで安心して(?)、1つの正弦波に対する電子回路の振る舞い、をみていくことにしましょう。
②インピーダンスという考え方
電子回路が正弦波に対してどのように振る舞うか、を考えるときに有効なのが、インピーダンスという考え方です。電子回路の振る舞いは、究極的には、加える電圧と流れる電流の関係といえます。ある部品に電圧Vを加えたとき、流れる電流Iとの関係がその部品の振る舞いを特徴づけるもの、ということができます。でもこれ、実は抵抗に対しては、「電気抵抗」と呼ぶ量なんですね。オームの法則から、V=IRですから、R=V/Iで定義される電気抵抗が「抵抗の特徴」といえます。
では、電子回路の基本的な部品であるコンデンサやインダクタに対するオームの法則はどうなるのでしょうか。コンデンサもインダクタも、直流に対してはまともに働きません。コンデンサに一定電圧を加えれば充電されて、満充電になったあとは電流が流れません。インダクタは、ただの導線ですから、一定電圧を加えても抵抗はゼロです。これらはいずれも定常状態になったあとの話です。
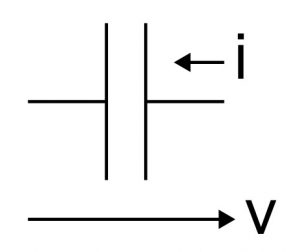
コンデンサに対する「オームの法則」
しかし、正弦波を加えたときは話が違います。電圧が変化すると、過渡現象としてそれにつられて電流も変化し、落ち着く前にまた電圧が変化して…ということが延々と続くことになります。そして、時間が十分にたったあとでは、このように変化している状態で安定した状況になるわけです。
数学的なテクニックを使うと、そのような安定した状況では、加える正弦波の電圧をv、流れる電流iに対して、その比であるv/iは、コンデンサやインダクタの素子値と正弦波の周波数で表されることが導かれます。v/iは、抵抗ならば抵抗値そのものですから、より一般的な「抵抗値のようなもの」と考えることができ、これを「インピーダンス」と呼びます。ちなみに正弦波の電圧や電流は小文字で表す、というルール(?)です。
コンデンサとインダクタのインピーダンスは、それぞれ1/jωC、jωLとなることが導かれます。ωは正弦波の角周波数という量で、正弦波の周波数f[Hz]の2π倍のことです。またjは虚数単位です。
「え?なんでここで虚数?」と思われる方も多いと思います。虚数は2乗すると-1になる量で、数学だと”i”という記号を使いますが、電気回路・電子回路では”i”は正弦波の電流を表す文字のため、”j”を使います。つまりj2=-1です。詳しい考え方や数学テクニックはここでは省略しますが「電圧と電流の変化のタイミング」(これを「位相」と呼びます)を表すのに、虚数を使うと都合がいいのです。
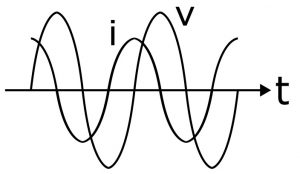
コンデンサに加える電圧vと流れる電流iの時間変化
コンデンサに加える電圧vと流れる電流iが時間とともにどのように変化するかを求めると、電圧の変化よりも電流のほうが少し前になり(電流が増えたあとで電圧が増える)、その変化のタイミングのズレは正弦波の周期の1/4となることが導かれます。この周期の1/4のズレが、数学テクニック上、虚数単位jで表すことができる、というわけです。このあたりの数学テクニックは、ちょっとこみいっているのですが、わかるととてもスッキリする考え方なので、興味のある方はぜひ調べてみてください。
いろいろな数学テクニックが出てきましたが、「正弦波で、コンデンサやインダクタの「抵抗」に相当する量をインピーダンスと呼んで、それぞれ1/jωCとjωLになる」ということだけ記憶に残してもらえれば十分です。
③ローパスフィルタとカットオフ周波数
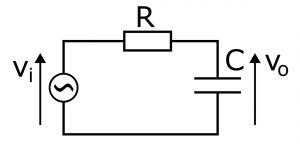
ローパスフィルタの回路
このような、抵抗とコンデンサからなる回路に正弦波の電圧viを加えたとき、コンデンサの電圧voがどうなるか、を考えてみましょう。といっても、いまは正弦波の電圧を加えた(そしてそれが十分に時間のたったあとで落ち着いている)状態ですから、「抵抗のようなもの」であるインピーダンスを使って考えることができます。つまりコンデンサも「抵抗値が1/jωCの抵抗”のようなもの”」と考えることができるのです。そうすると、この回路のvoは、viを2つの抵抗”のようなもの”で分圧した電圧、と考えることができます。
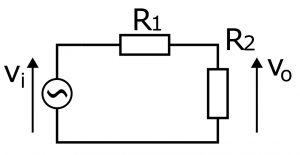
2つの抵抗による分圧
本当の抵抗であれば、分圧の法則を使えば vo/vi = R2 / (R1 + R2) となりますから、R2のところを抵抗”のようなもの”であるインピーダンスの(1/jωC)に置き換えれば、この回路は次のような式になります。
vo/vi = (1/jωC) / (R + 1/jωC)
これを整理すると、vo/vi = 1 / ( 1 + jωCR ) となります。これをHとおきましょう。Hは正弦波の角周波数ωで変わりますので、ωの関数という意味でH(ω)と書きましょう。ωが変わると、H(ω)がどのように変化するかを、この回路の「周波数特性」と呼びます。それは、関数のグラフを描けば、なんとなく概略がわかりそうです。しかし虚数が入った式なので、グラフを描くのもけっこう面倒です。
そこでまずはその絶対値|H(ω)|を考えることにしましょう。これは、vo/viの絶対値のことですから、与える正弦波と出てくる正弦波の振幅の比、つまり出てくる正弦波の振幅がどう変わるか、と考えることもできます。
これには、ちょっとしたうまいテクニックがあります。分母の実数部分(1)と虚数部分(ωCR)のどちらかが十分に大きい場合、を考えるのです。
まず「ωCRが1よりも十分に小さい」場合を考えましょう。この場合は、分母でωCRは、1よりも十分小さいので無視することができます。つまり分母はほぼ1となり、|H(ω)|=1、とみなすことが可能です。
逆に「ωCRが1よりも十分に大きい」場合は、1が無視できて、分母がjωCRのみとなり、|H(ω)|=1/ωCR、とみなすことができます。この場合の|H(ω)|はωに反比例、つまりωが大きくなるとどんどん小さくなっていくことになります。
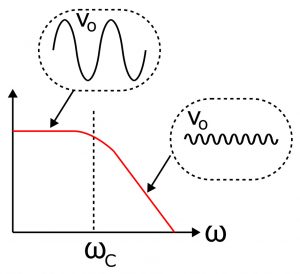
|H(ω)|のグラフとカットオフ周波数
この2つの場合の境目は1=ωCRのときで、それはω=1/CRの場合です。このωは、回路の特性が大きく変わる境界と考えることができますので、カットオフ(角)周波数ωCと呼びます。全体のグラフをかいてみると、たしかにカットオフ角周波数ωCを境にグラフの形が大きく変わっていることがわかります。
このグラフをみると、ωがωCよりも高い場合、つまりωCよりも高い角周波数の正弦波を与えた場合、出てくる正弦波の振幅は、ωを大きくするとどんどん小さくなっていくことになります。言い方を変えると周波数が低い(low)信号はそのまま通過させる(pass)、ともいえるので、このような回路をLow Pass Filter(LPF)と呼びます。
④方形波を入れると…
方形波をこの回路に与えてみましょう。ここではR=1kΩ、C=1μFとしています。この場合のカットオフ角周波数ωC=1/RC=1000です。これを周波数に換算したカットオフ周波数fCは、ωC/2π=159Hzとなります。
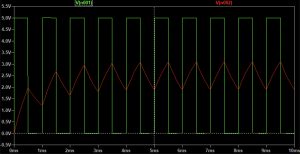
LPFに方形波を与えたときの出力波形(緑=vi、赤=vo)(回路シミュレータLTspiceで求めた波形)
与える方形波の周波数を1kHzとすると、このような波形になります。方形波の波形をフーリエ展開すると、1kHz, 3kHz, 5kHz, …といういろいろな周波数の正弦波に分解できます。それぞれにたいして|H(ω)|に応じた正弦波が出力voに現れますが、これらはいずれもfCよりも高い周波数なので、高い周波数ほどvoは小さくなっていきます。voは、1kHzの正弦波に、それより高い周波数の3kHz, 5kHz, …の正弦波も少し加わった波形になりますので、正弦波に微妙に周波数の高い正弦波を足した波形、になっているようになんとなく見えます。
ちなみに方形波をフーリエ展開すると、周波数がn倍の正弦波の比率は1/nになります。そしてfCよりも高い周波数では周波数がn倍になると|H(ω)|は1/n倍になります。つまり与える正弦波の周波数がn倍になると、voに出てくる正弦波の振幅は1/n2倍になるのです。これは実は三角波をフーリエ展開した結果と同じで、たしかにvoの波形は三角波になっていることがわかります。またこのシミュレーション結果で、最初の方ではvoが下の方にあるのが、徐々に上がっていき、真ん中あたりで落ち着く、という過渡現象もみられます。
「時間とともに変化する」という現象は、時間領域で考える過渡現象と、このように周波数領域で考える方法があります。それぞれ適した場面があるのですが、このあたりをみると、両者のつながりというか境界がみられるわけです。両者の使い分けというか、両者のつながりは、なかなか体得するのは大変なのですが、ぜひ慣れていただければと思います。
今回に連載はここまでとなります。お読み頂きましてありがとうございました!
今回の連載の流れ
第1回:抵抗の値を変えたら、なんか動いた(その1)
第2回:抵抗の値を変えたら、なんか動いた(その2)
第3回:抵抗の値を変えたら、なんか動いた(その3・今回)








