抵抗の値を変えたら、なんか動いた(その2)
電子工作をしていると「理屈はともかく、こうしておけ」と説明されるものがけっこうあります。とりあえず動くものをつくる分にはあまり困らないことが多いですが、「なんで?」とモヤモヤする方も多いかと思います。あるいはうまく動かないとき、闇雲に適当に手を入れて、とりあえず動いたからまあいいか、としている場合もあるのではないでしょうか。より踏み込んだ電子回路をつくるようになると、それらの「理屈」がけっこう効いてくる場面もあります。
第1回では、LEDにつなぐ電流制限抵抗を手始めに、電子回路の中での抵抗の役割について詳しくみてきました。そこから、与える電圧と流れる電流の関係を深く理解することができたと思います。
電子回路を使う上で、もう1つの大切な見方が「電圧や電流が、時間とともにどう変化するか」という観点です。その変化が予想からずれると予期しない誤作動の原因にもなって、デバッグするのが厄介なこともよくあります。そしてここでも、抵抗の働きが効いてきます。
目次
①ArduinoのanalogWrite()からアナログ電圧へ
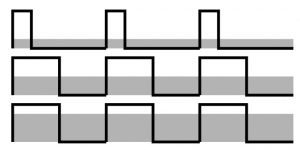
Arduinoの機能に、アナログ電圧を出力するanalogWrite()というのがあります。ただ、これは、D/A変換器で指定した電圧を出力するものではなく、PWM信号というものを使います。
PWM (Pulse Width Modulation)というのは、パルスの周期の”1”と”0”の時間の割合で、「平均的な」ONの時間を決める方式です。例えば”1”と”0”の時間が同じであれば、平均的には”0.5”になるだろう、というもの。実際、ここにLEDをつなぐと、”1”のときだけLEDに電流が流れて点灯するため、”1”の時間の比率が高いほど明るくなります。
と、ここまで読んだところで、PWM出力はONの時間の割合が変わるだけで、実際に電圧が変わるわけではない、ということに気づいた方もいるでしょう。実際そのとおりで、例えば電圧計でPWM出力の端子の電圧を測っても、厳密にはanalogWrite()で指定した値に比例する一定の電圧が現れるわけではありません。LEDの明るさが変わるのは、LEDがPWM出力の周期で点滅しているのに、あまりにも速く見た目では点滅しているようには見えず、実際に点灯している”1”の時間の比率が高いほど明るく見える、ということなのです。
②速い変化と遅い変化の境界はどこ?
ところで「一定の電圧」とは、どういうことでしょうか。時間とともに変化しない電圧や電流を「直流」と呼び、これが「一定の電圧」です。電圧計で測れば、変化せずに一定の値となる、ものです。
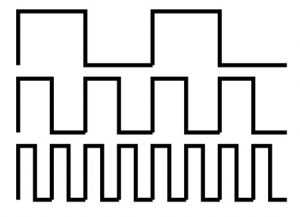
では、5秒ごとにゆっくり”1”と”0”を繰り返す電圧波形を電圧計で測ると、どのように見えるでしょうか。5秒ごとに高い電圧(例えば5V)と低い電圧(0V)が計測されるでしょう。
1秒ごとだとどうなるでしょう?0.1秒だと…?変化がゆっくりなうちは電圧計がそれぞれの電圧を表示できますが、速くなるにつれて電圧計が追いつかなくなってしまいます。5Vを表示しようとしているうちに出力波形が0Vになり、あわてて0Vを表示しようとして…ということがおこるでしょう。
つまり、電圧計が「追いつける」くらい遅い変化であれあれば、その間は「一定の電圧」をみなすことができます。そして「追いつけない」くらい速い変化になると、正しい計測ができなくなります。
では、「追いつける」と「追いつけない」の境界はどこなのでしょうか。どのような回路でも、電流が流れると電圧が変化しますが、その電圧の変化にはある時間がかかります。例えばLEDを(電流制限抵抗をつないで)電源につなぐと、一瞬で点灯するように見えます。しかし本当は、一瞬つくのではなく、ケーブルの中を電子が流れていく際、ケーブル各所の電圧が少しずつ変化し、それが最終的にLEDまで到達したあと電流が流れて点灯するのです。
もちろん、この現象は目で見ていてもわからないほど速いため、一瞬で点灯するように見えます。このように電圧が少しずつ変化する現象を「過渡現象」といいます。電子回路の中での電圧や電流の変化は、ミクロで見るとすべて、この「過渡現象」が起こっているわけです。そして変化が落ち着くと一定の電圧・電流になります(この状態を「定常状態」といいます)。
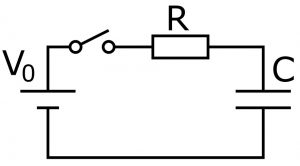
このような電圧が少しずつ変化していく現象は、出力波形の電圧源が、抵抗を通してコンデンサにつながった回路でモデル化することができます。電子部品としてのコンデンサでなくても、ケーブルだけで、接地面(グランド)に対する静電容量が必ず生じますので、コンデンサがつながっていると考えることができるわけです。そして、どのようなケーブルにも電気抵抗が必ずあるので、抵抗とコンデンサの回路としてモデル化できるのです。
ちなみに高校で物理を学んだことがある方なら、こんな問題を考えたことがあるはずです(この部分は本題とあまり関係ないので、興味のない方は読み飛ばしてOKです)。
2つの同じ静電容量Cのコンデンサのうち、1つがVで充電され、もう1つは電荷がない状態から両者を接続すると、蓄えられているエネルギーはどうなるでしょうか。最初の状態では、充電されたほうの電荷がQ=CVなので蓄えられたエネルギーはCV2/2、もう片方は電荷がないので0です。接続した後は電荷の移動が起こって2つのコンデンサは同じ電圧V/2になりますので、それぞれのコンデンサのエネルギーはC(V/2)2/2=CV2/8、2つをあわせてCV2/4となって、最初の状態よりもエネルギーが減っています。このエネルギーはどこへ行ってしまったのでしょうか?
答えを言ってしまうと、この接続に抵抗Rを使うとすれば電荷の移動にともなって、抵抗でジュール熱が発生してエネルギーが失われます。これを求めるとちょうどCV2/4となり、コンデンサに蓄えられたエネルギーの変化分と同じになって辻褄があいます。そしてRを0に近づける極限を求めてもこの結果は変わりません。
さて、さきほどの抵抗を通してコンデンサを充電する回路で、コンデンサの電圧が時間とともにどのように変化するかは、微分方程式で求めることができます。詳細を知りたい方は電気回路に関する書籍をみていただくことにして、結果だけ書いておくと次のような式になり、グラフは図のようになります。ちなみにeは自然対数の底で2.718…ですが、まああまり細かいことは気にしなくて大丈夫です。
VC(t) = V0 (1 – e– t / RC )
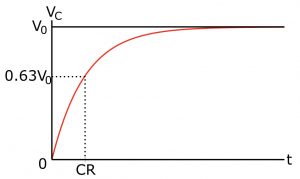
このグラフから、コンデンサの電圧は少しずつあがっていき、最終的に電圧源と同じ電圧になる(これが定常状態)ことがわかります。そしてこの電圧変化の様子が「過渡現象」です。変化の「速さ」を特徴づけるパラメータが抵抗の値とコンデンサの容量の積、つまり”CR”です。さきほどの式を使って求めると、変化の始まりの点における接線と最終電圧との交点の時間がCRとなり、そのときの電圧は最終電圧の0.63倍(1-1/e倍)になることが求められます。
ポイントは「コンデンサの電圧が、まあまあ大きく(最終電圧の0.63倍)なるまでにかかる時間が”RC”」ということです。つまり”RC”は、この回路でコンデンサが充電されるのにかかる時間の目安、といえますので、この”RC”を「時定数(じていすう)」と呼びます。
この時定数は、回路の電圧の変化にかかる時間の目安、となります。これよりも長い時間がたてば「まあ電圧変化も落ち着いているので、一定(定常状態)とみなせなくはない」状態です。逆にこれよりも短い時間では「まだ変化している途中(過渡状態)」ということに。つまりこの時定数が、「定常状態」と「過渡状態」との境界の時間の目安、といえます。
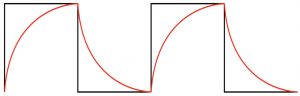
加える電圧を時間とともに素早く切り替えると、充電と放電が交互に起こります。しかし電圧の変化で一定電圧になっている時間が時定数よりもなが長ければ、コンデンサの電圧の変化が追いつきますので、コンデンサの電圧も充電と放電にあわせた変化が十分に見えます。
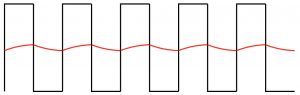
一方、変化が速くなって、一定電圧の時間が時定数よりも短くなると、コンデンサの電圧変化が追いつけず、十分に上がり切る前に下り始めてしまい、変化が小さくなってしまうでしょう。つまり定常状態に近づきます。この「定常状態」になる電圧は、放電の電圧よりも充電の時間が長いほど、高くなりそうだと直感的に思えますが、実際に計算した結果もそうなります。そして電圧が、充電と放電の時間の比、つまりPWM波形の”1”と”0”の時間の比率(デューティー比)で決まることが導かれるでしょう。
ここまでみてきたように、PWM波形は、つながっている(とみなせる)コンデンサの容量と抵抗の値から決まる時定数よりも長い周期であれば、一定電圧とみなすことができます。ちなみにPWM波形のデューティー比が変わったときにも過渡現象が起こり、変化の速さも時定数で決まることが導かれます。つまりCやRが大きくて時定数が大きいほど、PWM波形のデューティー比のゆっくりな変化にしか追いつけない、ということです。
このあたりは、別の見方で考えることもできますが、それについては次回、詳しく見ていきましょう。
③ダンピング抵抗
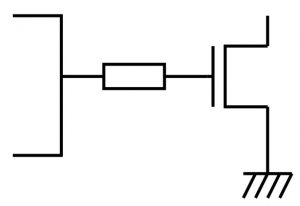
この時定数に関係する現象で、電子回路ではときどき「とりあえず動く」になりがちなものに「ダンピング抵抗」があります。ダンピング抵抗は、MOSトランジスタのように大きいな容量をもつ負荷を”1”/”0”で駆動するときに、直列につなぐべき抵抗です。「とりあえず100ΩぐらいをつないでおけばOK」と書いてある情報も散見されます。

Alpha and Omega社のAO3400Aのデータシートより
大きな電流を小さな素子でON/OFFできるパワーMOSトランジスタの制御端子であるG(ゲート)は、一般に大きなコンデンサとみなせて、1nFくらいのものもよくあります。
さきほどの時定数を求めた回路で、コンデンサの充電が始まるときに流れる電流も、最初はコンデンサの電荷が0で電圧も0なので、抵抗Rで決まります。つまりRが小さいほど最初の流れはじめの電流が大きいわけです。そしてあまり電流が大きすぎると、駆動する側のマイコンの消費電流が大きく変化することになり、場合によっては電源ラインの電圧変化になってマイコンにリセットがかかったりすることも、よくあります。
そこで、あえて100Ωくらいの抵抗をつないでおくと、最初の充電電流が小さくなって、電源ラインの電圧変化を抑えることができるのです。もちろん充電にかかる時間は時定数で決まりますから、ここに抵抗をつなぐと、電圧変化が遅くなってしまいます。しかしあえて「変化を遅くする」ことで、「変化の影響」を小さくすることは可能です。このような抵抗を「ダンピング抵抗」といいます。多くの場合は100Ωで大丈夫なことが多いようですが、挙動が怪しいときは、はオシロで波形を観測しながら、変化速度と電流変化の兼ね合いからダンピング抵抗の値を調整するとよいでしょう。
今回はここまで。次回もお楽しみに!
今回の連載の流れ
第1回:抵抗の値を変えたら、なんか動いた(その1)
第2回:抵抗の値を変えたら、なんか動いた(その2・今回)
第3回:抵抗の値を変えたら、なんか動いた(その3)








